
2016年に IBM が IBM Q Experience として 5量子ビットの量子コンピュータをクラウド上に無料で開放して数年、Microsoft の Azure Quantum と Amazon の Amazon Bracket が、限定公開ながら相次いで発表されました。量子コンピュータが誰でも使える環境が整いつつあります。
動作原理が現行コンピュータとは根本から異なる上に、現時点ではアセンブラレベルのプログラミング言語しか用意されておらず、しかも実用的なアプリケーションへの適用がまだできないと、3重苦のような環境ですが、20年後は日常的に使われているのではないかと夢想します。
といっても、今の機械学習がアルゴリズムの詳細を理解しなくても使えるように、量子プログラミングもライブラリを呼ぶだけになるのだと思います。論理回路を知らなくてもウェブサイトは作れるし、イーサネットケーブルを流れる信号について知らなくても HTTP で通信できます。
知らなくても使える。でも知らないで使うのは嫌なので、20年後を目指して、量子プログラミングの勉強をすることにしました。
目次
量子コンピュータのプログラム
アセンブラまたは論理回路で作る感覚です。IBM Q Experience では、以下のような図でプログラムを表現します。
Python や JavaScript のライブラリとして実装されているものもありますし、Microsoft が専用に開発した Q# 言語というものもあります。一見高級言語が使えるようでいて、実際はアセンブラのように量子ビット(Qubit、キュービット)の操作をします。論理回路が AND、OR、NOT の基本ゲートの組み合わせで何でも作れるように、量子コンピュータのプログラムもゲートの組み合わせで作ります。
0 の量子ビットをそのまま読み出す
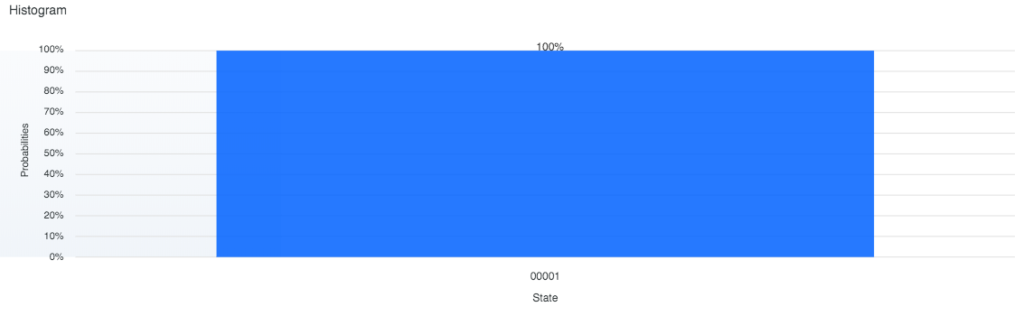
量子ビットは |0> や |1> という表記で表します。「ケットベクトル」と呼びます。この記法は、ノーベル物理学賞を受賞したイギリスの物理学者ディラックによる発明です。古典コンピュータ(今のコンピュータという意味)での 0 は |0> で、1 は |1> で表します。|0> を読み出すと 0 になるということを確かめます。プログラムはこちら。
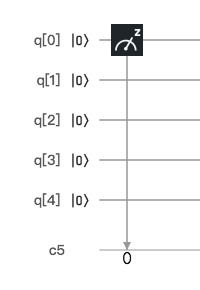
5量子ビット定義されているうちの、1量子ビットのみ使っています。プログラムは左から右に向かって実行されます。初期状態として |0> が設定されています。これをそのまま、メーターのようなものに z と書いてある命令で読み出します。この四角形を「ゲート」と呼びます。シミュレータで実行すると、以下の結果が得られます。
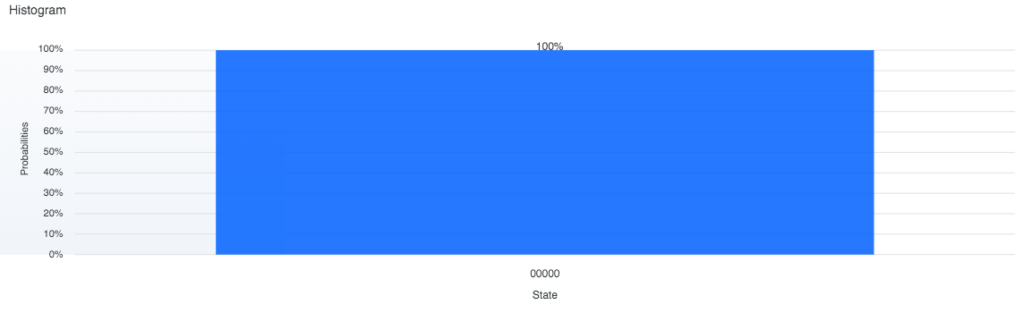
1024回実行して、00000 が 100% 得られました。当然です。
NOTゲートで反転して読み出す
今度は NOTゲートで反転してみましょう。IBM Q Experience には NOTゲートというものは定義されていませんが、量子ビットを球で表現できると考えた時に(ブロッホ球という)、量子ビットを X軸を中心に 180度回転させる Xゲートというものがあります。これが |0> を |1> にする効果を持っており、古典論理回路の NOTゲートに相当します。プログラムはこちら。
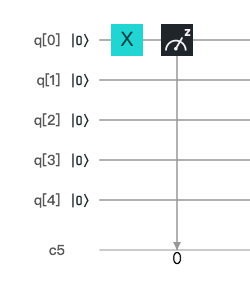
実行すると 00001 が 100% 得られます。当然です。
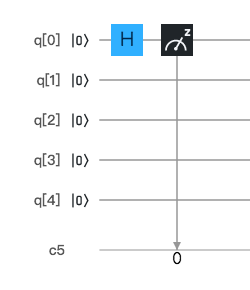
|0> と |1> の重ね合わせ状態を作る
ここからようやく量子コンピュータっぽくなります。量子ビットは、|0> や |1> という特定の状態だけではなく、その「重ね合わせ状態(superposition)」を持つことができます。確率的に 0 でもあるし 1 でもあるという状態です。
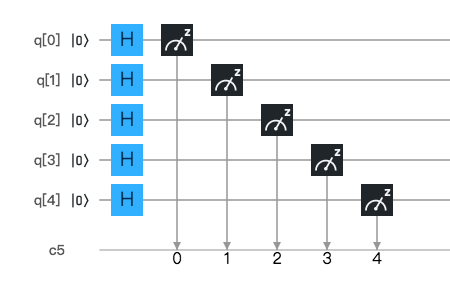
プログラムはこちらです。Hゲートを使います。アダマールゲートと呼びます。フランスの数学者ジャック・アダマール(Hadamard)に因んでいます。多くの量子プログラムで、量子ビットの初期化に使われます。
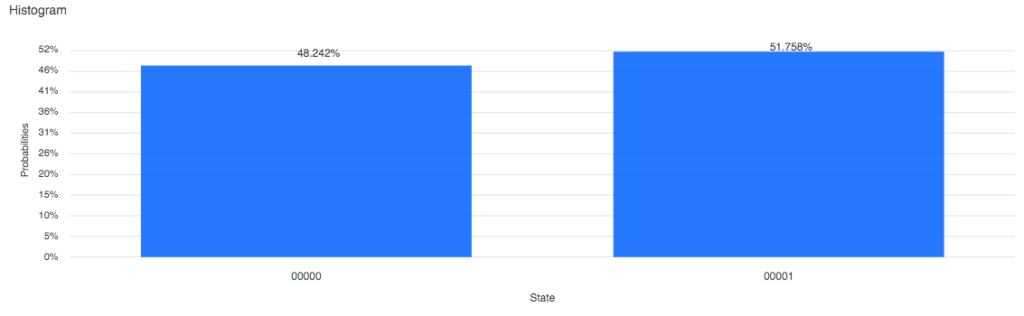
シミュレータでの実行結果はこちらです。00000 と 00001 が、それぞれ約50%の確率で観測されました。
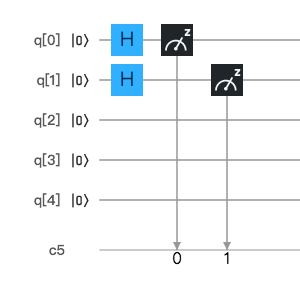
2量子ビット
同じことを 2量子ビットで実行するとどうなるでしょうか。Hゲートを 2つの量子ビットに適用してみます。
結果はこちらです。
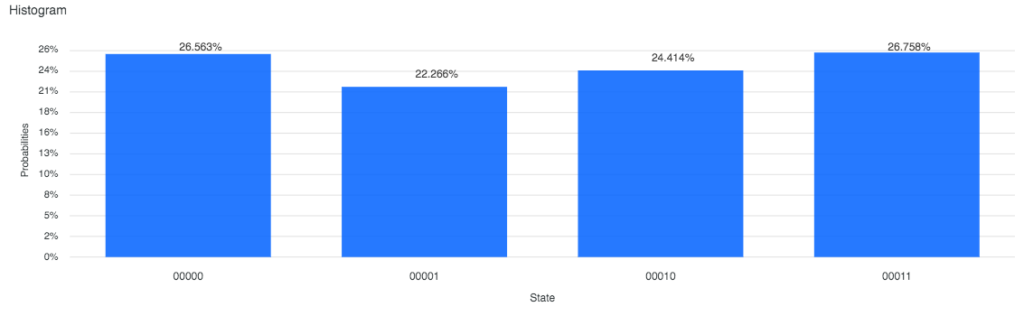
00000、00001、00010、00011 が、それぞれ約25%ずつ観測されました。つまり、2量子ビットで、同時に4つの可能性を表現しています。
5量子ビット
5量子ビットでも同じことをしてみます。

結果はこちらです。全部表示しきれず、一部が省略されていますが、00000 から 11111 まで、32状態を同時に持っています。
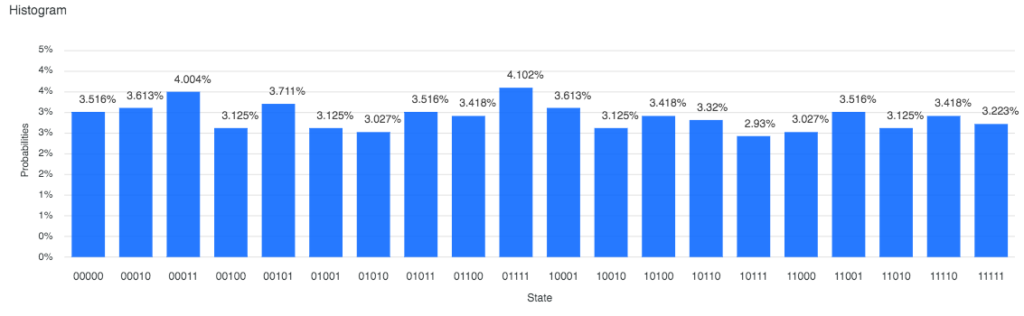
この複数の可能性に対して同時に演算を実行できるのが、量子コンピュータの強みです。量子コンピュータの超並列計算とも言われます。1量子ビットで 2状態、2量子ビットで 4状態、5量子ビットで 32状態を同時に持ちます。つまり 2^n の状態を持てます。
それはすごいことなのか
1量子ビットは、複素数2つで表現されます。古典コンピュータでシミュレーションするために、これを32バイトで表現するとします(『驚異の量子コンピュータ』より)。2量子ビットの表現には64バイト、10量子ビットには16キロバイト、20量子ビットで16メガバイト、30量子ビットで16ギガバイト、40量子ビットで16テラバイト、50量子ビットのシミュレーションには16ペタバイトの記憶装置が必要です。
2019年10月に、Google が 53量子ビットのコンピュータで、従来のコンピュータを凌駕したという発表をしました。量子コンピュータで200秒かかるタスクが、スーパーコンピュータで1万年かかる、というのです。IBM がそれに対して、いや、2日半で処理できると反論しました。しかし、古典コンピュータでシミュレーションできるのは、このあたりが限界になりそうです。1量子ビット増えるたびに、倍の記憶装置が必要になります。
量子ビットの数は指数関数的に増え続けていて、2014年に 5量子ビットが実現、2015年 9量子ビット、2017年 22量子ビット、2018年 72量子ビット、2019年 79量子ビットが実現されています。2025年には 1万量子ビット、2030年には100万量子ビットが実現されるかもしれません。
量子コンピュータのアプリケーションの1つとして、ショアのアルゴリズムによる大きな数の素因数分解が有名です。公開鍵暗号のRSA鍵が 2048ビットや 4096ビットで作られていることを考えると、数年後の未来に数千量子ビットが実用化されたとき、暗号化方式の変更を迫られそうです。






